5  The submodel trick

Note

While this chapter is an early draft, it’s relatively complete and should be coherent for readers.

In Section 1.1.3, I created a custom grid of parameters, rather than relying on tidymodels’ default grid generation, to enable something I referred to as the “submodel trick.” The submodel trick allows us to evaluate many more models than we actually fit; given that model fitting is the most computationally intensive operation when resampling models (by far), cutting out a good few of those fits results in substantial time savings. This chapter will explain what the submodel trick is, demonstrating its individual contribution to the speedup we saw in Section 1.1.3 along the way. Then, I’ll explain how users can use the submodel trick in their own analyses to speed up the model development process.

5.1 Demonstration

Recall that, in Section 1.1.2, we resampled an XGBoost boosted tree model to predict whether patients would be readmitted within 30 days after an inpatient hospital stay. Using default settings with no optimizations, the model took 3.68 hours to resample. With a switch in computation engine, implementation of parallel processing, change in search strategy, and enablement of the submodel trick, the time to resample was knocked down to 1.52 minutes. What is the submodel trick, though, and what was its individual contribution to that speedup?

First, loading packages and setting up resamples and the model specification as before:

# load packages
library(tidymodels)
library(readmission)

# load and split data:
set.seed(1)
readmission_split <- initial_split(readmission)
readmission_train <- training(readmission_split)
readmission_test <- testing(readmission_split)
readmission_folds <- vfold_cv(readmission_train)

# set up model specification
bt <- 
  boost_tree(learn_rate = tune(), trees = tune()) %>%
  set_mode("classification")

5.1.1 Grids

If I just pass these resamples and model specification to tune_grid(), as I did in Section 1.1.2, tidymodels will take care of generating the grid of parameters to evaluate itself. By default, tidymodels generates grids of parameters using an experimental design called a latin hypercube (McKay, Beckman, and Conover 2000; Dupuy, Helbert, and Franco 2015). We can use the function grid_latin_hypercube() from the dials package to replicate the same grid that tune_grid() had generated under the hood:

set.seed(1)
bt_grid_latin_hypercube <- 
  bt %>%
  extract_parameter_set_dials() %>%
  grid_latin_hypercube(size = 12)

bt_grid_latin_hypercube

# A tibble: 12 × 2
   trees learn_rate
   <int>      <dbl>
 1   647    0.164  
 2   404    0.0555 
 3  1798    0.0452 
 4   796    0.274  
 5  1884    0.00535
 6  1139    0.00137
 7  1462    0.105  
 8  1201    0.00194
 9   867    0.0225 
10   166    0.00408
11   326    0.0116 
12  1608    0.00997

Since we’re working with a two-dimensional grid in this case, we can plot the resulting grid to get a sense for the distribution of values:

ggplot(bt_grid_latin_hypercube) +
  aes(x = trees, y = learn_rate) +
  geom_point()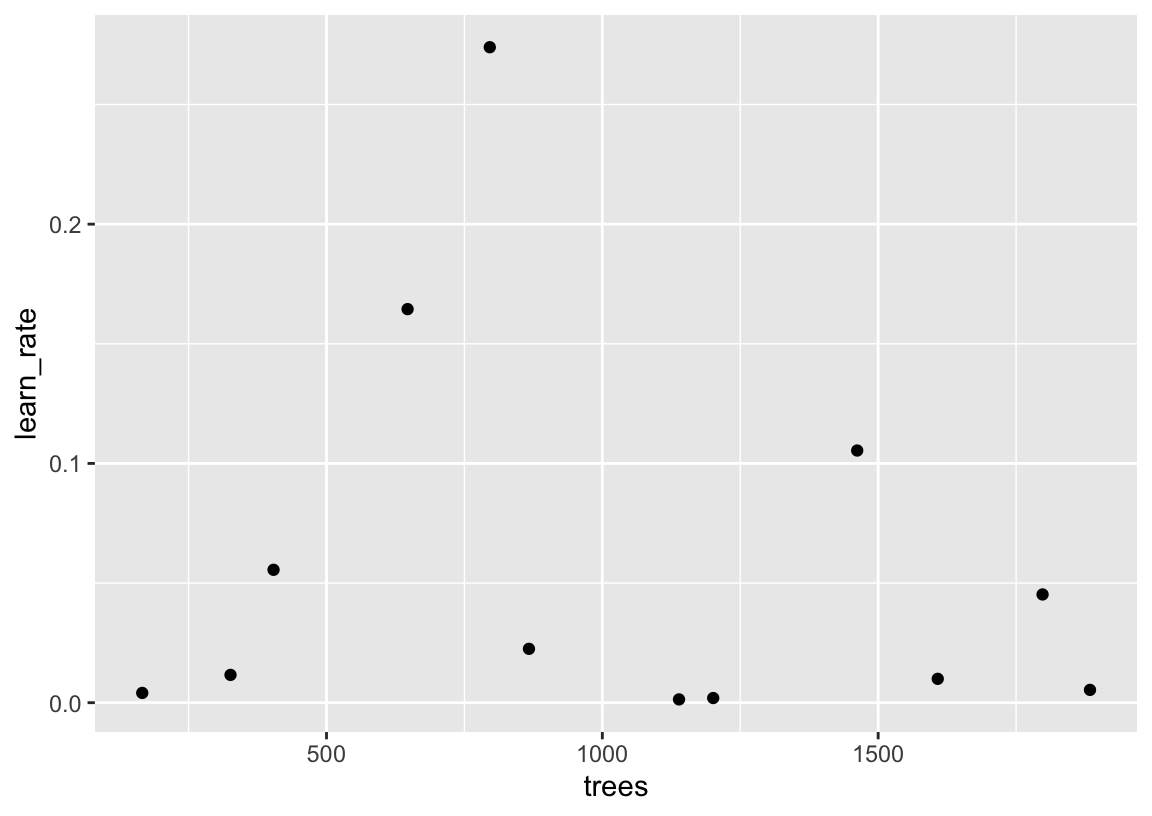

Distribution of proposed boosted tree hyperparameters, generated using a semi-random latin hypercube design. Notably, values in neither the x or y axes appear more than once.

While the details of sampling using latin hypercubes are not important to understand this chapter, note that values are not repeated in a given dimension. Said another way, we get 12 unique values for trees, and 12 unique values for learn_rate. Juxtapose this with the design resulting from grid_regular() used in Section 1.1.3:

set.seed(1)
bt_grid_regular <-
  bt %>%
  extract_parameter_set_dials() %>% 
  grid_regular(levels = 4)

bt_grid_regular

# A tibble: 16 × 2
   trees learn_rate
   <int>      <dbl>
 1     1    0.001  
 2   667    0.001  
 3  1333    0.001  
 4  2000    0.001  
 5     1    0.00681
 6   667    0.00681
 7  1333    0.00681
 8  2000    0.00681
 9     1    0.0464 
10   667    0.0464 
11  1333    0.0464 
12  2000    0.0464 
13     1    0.316  
14   667    0.316  
15  1333    0.316  
16  2000    0.316  

Plotting in the same way:

ggplot(bt_grid_regular) +
  aes(x = trees, y = learn_rate) +
  geom_point()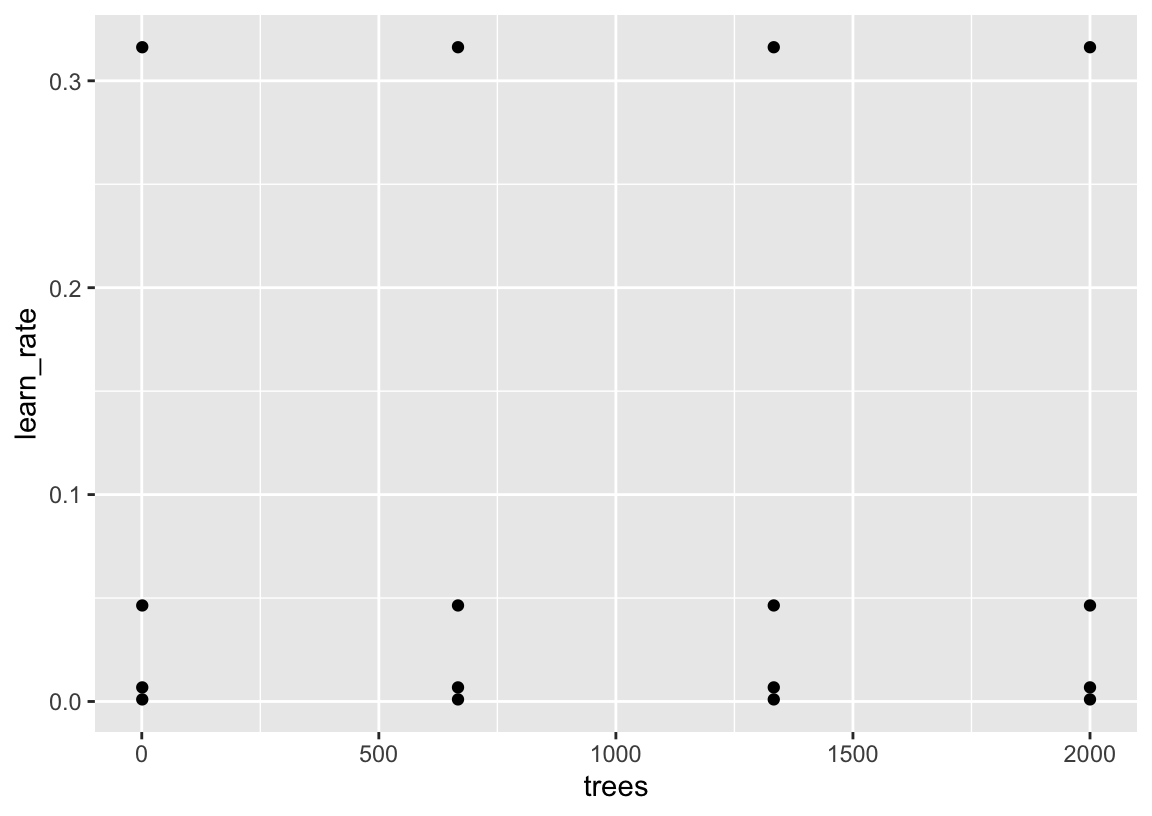

Distribution of proposed boosted tree hyperparameters, generated using a regular grid. There are 4 unique levels of both the trees and learn_rate parameters, and the grid is formed by taking unique combinations of them.

The argument levels = 4 indicates that \(4\) values are generated individually for each parameter, and the resulting grid is created by pairing up each unique combination of those values.

You may have noticed that this regular grid contains even more proposed points—4 x 4 = 16—than the latin hypercube with size = 12. A reasonable question, then: how on earth would the larger grid be resampled more quickly than the smaller one? It’s possible that I hid some slowdown resulting from this larger grid among the rest of the optimizations implemented in Section 1.1.3; lets test the effect of the change in grid by itself.

set.seed(1)

bm_grid_regular <- 
  bench::mark(
    grid_regular = 
      tune_grid(
        object = bt,
        preprocessor = readmitted ~ .,
        resamples = readmission_folds,
        grid = bt_grid_regular
      )
  )

bm_grid_regular

# A tibble: 1 × 3
  expression   median mem_alloc
* <bch:expr> <bch:tm> <bch:byt>
1 basic         1.23h    3.91GB

See? Have some faith in me!

Changing only the grid argument (and even increasing the number of proposed grid points), we’ve decreased the time to evaluate against resamples from 3.68 to 1.23 hours, or a speedup of 67%.

5.1.2 The trick

Passing this regular grid allowed tune_grid() to use what the tidymodels team refers to as the “submodel trick,” where many more models can be evaluated than were actually fit.

To best understand how the submodel trick works, let’s refresh on how boosted trees work. The training process begins with a simple decision tree, and subsequent trees are added iteratively, each one correcting the errors of the previous trees by focusing more on the data points associated with the greatest error. The final model is a weighted sum of all the individual trees, where each tree contributes to reducing the overall error.

So, for example, to train a boosted tree model with 2000 trees, we first need to train a boosted tree model with 1 tree. Then, we need to take that model, figure out where it made its largest errors, and train a second tree that aims to correct those errors. So on, until the, say, 667-th tree, and so on until the 1333-rd tree, and so on until, finally, the 2000-th tree. Picking up what I’m putting down? Along the way to training a boosted tree with 2000 trees, we happened to train a bunch of other models we might be interested in evaluating: what we call submodels. So, in the example of bt_grid_regular, for a given learn_rate, we only need to train the model with the maximum trees. In this example, that’s a quarter of the model fits.

Note

You might note that we don’t see a speedup nearly as drastic as 4 times. While we indeed only fit a quarter of the models, we’re fitting the boosted trees with the largest number of trees, and the time to train a boosted tree scales linearly with the number of trees. Said another way, we’re eliminating the need to fit only the faster-fitting models. This tends to be the case in many cases where the submodel trick applies.

To evaluate a fitted model with performance metrics, all we need are its predictions (and, usually, the true values being predicted). In pseudocode, resampling a model against performance metrics usually goes something like this:

for (resample in resamples) {
  # analogue to the "training" set for the resample
  analysis <- analysis(resample)
  # analogue to the "testing" set for the resample
  assessment <- assessment(resample)
  
  for (model in models) {
    # the longest-running operation:
    model_fit <- fit(model, analysis)
    
    # usually, comparatively quick operations:
    model_predictions <- predict(model_fit, assessment)
    metrics <- c(metrics, metric(model_predictions))
  }
}

Note

analysis(), assessment(), fit(), and predict() are indeed actual functions in tidymodels. metric() is not, but an analogue could be created from the output of the function metric_set().

Among all of these operations, fitting the model with fit() is usually the longest-running step, by far. In comparison, predict()ing on new values and calculating metrics takes very little time. Using the submodel trick allows us to reduce the number of fit()s while keeping the number of calls to predict() and metric() constant. In pseudocode, resampling with the submodel trick could look like:

for (resample in resamples) {
  analysis <- analysis(resample)
  assessment <- assessment(resample)
  
  models_to_fit <- models[unique(non_submodel_args)]
  
  for (model in models_to_fit) {
    model_fit <- fit(model, analysis)
    
    for (model_to_eval in models[unique(submodel_args)]) {
      model_to_eval <- predict(model_to_eval, assessment)
      metrics <- c(metrics, metric(model_predictions))
    }
  }
}

The above pseudocode admittedly requires some generosity (or mental gymnastics) to interpret, but the idea is that if fit()ting is indeed the majority of the time spent in resampling, and models_to_fit contains many fewer elements than models in the preceding pseudocode blocks, we should see substantial speedups.

5.1.3 At its most extreme

In the applied example above, we saw a relatively modest speedup. If we want to really show off the power of the submodel trick, in terms of time spent resampling per model evaluated, we can come up with a somewhat silly grid:

bt_grid_regular_go_brrr <-
  bt_grid_regular %>%
  slice_max(trees, by = learn_rate) %>%
  map(.x = c(1, seq(10, max(.$trees), 10)), .f = ~mutate(.y, trees = .x), dfr = .) %>%
  bind_rows()

bt_grid_regular_go_brrr

# A tibble: 804 × 2
   trees learn_rate
   <dbl>      <dbl>
 1     1    0.001  
 2     1    0.00681
 3     1    0.0464 
 4     1    0.316  
 5    10    0.001  
 6    10    0.00681
 7    10    0.0464 
 8    10    0.316  
 9    20    0.001  
10    20    0.00681
# ℹ 794 more rows

In this grid, we have the same number of unique values of learn_rate, \(4\), resulting in the same \(4\) model fits. Except that, in this case, we’re evaluating every model with number of trees \(1, 10, 20, 30, 40, ..., 2000\). If our hypothesis that predicting on the assessment set and generating performance metrics is comparatively fast is true, then we’ll see that elapsed time per grid point is way lower:

set.seed(1)

bm_grid_regular_go_brrr <- 
  bench::mark(
    grid_regular_go_brrr = 
      tune_grid(
        object = bt,
        preprocessor = readmitted ~ .,
        resamples = readmission_folds,
        grid = bt_grid_regular_go_brrr
      )
  )

The above code took 1.44 hours to run, a bit longer than the 1.23 hours from bm_grid_regular (that fitted the same number of models), but comparable. Per grid point, that difference is huge:

# time per grid point for bm_grid_regular
bm_grid_regular$median[[1]] / nrow(bt_grid_regular)

[1] 4.62m

# time per grid point for bm_grid_regular_go_brrr
bm_grid_regular_go_brrr$median[[1]] / nrow(bt_grid_regular_go_brrr)

[1] 6.44s

Whether this difference in timing is of practical significance to a user is debatable. In the context where we generated bm_grid_regular, where the grid of points searched over is relatively comparable (and thus similarly likely to identify a performant model) yet the decreased number of model fits gave rise to a reasonable speedup—-99.67%—is undoubtedly impactful for many typical use cases of tidymodels. The more eye-popping per-grid-point speedups, as with bm_grid_regular_go_brrr, are more so a fun trick than a practical tool for most use cases.

5.2 Overview

I’ve demonstrated the impact of the submodel trick in the above section through one example context, tuning trees in an XGBoost boosted tree model. The submodel trick can be found in many places across the tidymodels framework, though.

Submodels are defined with respect to a given model parameter, e.g. trees in boost_tree(). While a given parameter often defines a submodel regardless of modeling engine for a given model type—e.g. trees defines submodels for boost_tree() models regardless of whether the model is fitted with engine = "xgboost" or engine = "lightgbm"—there are some exceptions. Many tidymodels users undoubtedly tune models using arguments that define submodels without even knowing it. Some common examples include:

• penalty in linear_reg(), logistic_reg(), and multinom_reg(), which controls the amount of regularization in linear models.

• neighbors in nearest_neighbor(), the number of training data points nearest the point to be predicted that are factored into the prediction.

Again, some modeling engines for each of these model types do not actually support prediction from submodels from the noted parameter. See Section 5.2.1 for a complete table of currently supported arguments defining submodels in tidymodels.

In the above example, we had to manually specify a grid like bt_regular_grid in order for tidymodels to use a grid that can take advantage of the submodel trick. This reflects the frameworks’ general prioritization of predictive performance over computational performance in its design and defaults; latin hypercubes have better statistical properties when it comes to discovering performant hyperparameter combinations than a regular grid (McKay, Beckman, and Conover 2000; Stein 1987; Santner et al. 2003). However, note that in the case where a model is being tuned over only one argument, the submodel trick will kick in regardless of the sampling approach being used: regardless of how a set of univariate points are distributed, the most extreme parameter value (e.g. the max trees) can be used to generate predictions for values across the distribution.

5.2.1 Supported parameters

A number of tuning parameters support the submodel trick:

Model Type	Argument	Engines
boost_tree	trees	xgboost, C5.0, lightgbm
C5_rules	trees	C5.0
cubist_rules	neighbors	Cubist
discrim_flexible	num_terms	earth
linear_reg	penalty	glmnet
logistic_reg	penalty	glmnet
mars	num_terms	earth
multinom_reg	penalty	glmnet
nearest_neighbor	neighbors	kknn
pls	num_comp	mixOmics
poisson_reg	penalty	glmnet
proportional_hazards	penalty	glmnet
rule_fit	penalty	xrf

Dupuy, Delphine, Céline Helbert, and Jessica Franco. 2015. “DiceDesign and DiceEval: Two r Packages for Design and Analysis of Computer Experiments.” Journal of Statistical Software 65 (11).

McKay, Michael D, Richard J Beckman, and William J Conover. 2000. “A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code.” Technometrics 42 (1): 55–61.

Santner, Thomas J, Brian J Williams, William I Notz, and Brain J Williams. 2003. The Design and Analysis of Computer Experiments. Vol. 1. Springer.

Stein, Michael. 1987. “Large Sample Properties of Simulations Using Latin Hypercube Sampling.” Technometrics 29 (2): 143–51.